Warum Grundlagen wichtig sind und Spaß machen

Wer das Programmieren lernen möchte, ist meist hoch motiviert und hat idealerweise schon eine Projektidee im Kopf, an der er seine neuen Fähigkeiten ausprobieren möchte. Da bleibt nicht viel Zeit, um sich mit Mathematik und Rechnerarchitekturen zu beschäftigen – und das ist für den Anfang auch völlig okay. Aber wer professionell Software entwickeln möchte, kommt um die Grundlagen nicht herum.
Für einen Programmierer gibt es viele Einsatzgebiete und in jedem Einsatzgebiet gibt es viele Programmierer, die der Aufgabe gewachsen sind. Eine Vielzahl an frei verfügbaren Frameworks, Blogbeiträgen und Codebeispielen erleichtern die Arbeit und machen es überflüssig, sich mit den Details auseinanderzusetzen, aber …
Aber es lohnt sich, sich mit den Details auseinanderzusetzen. Ein Verständnis für die Arbeitsweise von Rechnern und Grundlagen der Mathematik wird immer dann wertvoll, wenn das Programm zu langsam ist, dem Zielsystem der Speicher ausgeht oder ganz klassisch irgendetwas nicht funktioniert.
Mittlerweile werden viele unkritische Programmieraufgaben in Billiglohnländer ausgelagert und wer auf Dauer in Deutschland konkurrenzfähig bleiben will, braucht Grundlagen, die dabei helfen, Standardfunktionalität effizienter und zuverlässiger zur Verfügung zu stellen.
Als Beispiel müssen heute Vektoren der klassischen Mathematik herhalten. Warum? Sie tauchen überall auf und ich werde euch zwei Beispiele aus völlig unterschiedlichen Anwendungsbereichen zeigen:

Abstände von 3D-Objekten in Videospielen

Zuerst ein kleiner Einblick in die Videospieleentwicklung. Dabei ist es egal, ob das Spiel für den PC, die PlayStation, die XBOX oder eine andere Plattform erstellt werden soll. Für die Entwicklung eines Spiels, egal ob 2D oder 3D ist ein Verständnis von Vektoren zumeist unerlässlich. Vektoren werden dazu genutzt, um z.B. einen Punkt im Raum zu definieren oder eine Bewegung, indem der Vektor in die Bewegungsrichtung zeigt und seine Länge die Bewegungsgeschwindigkeit definiert. In modernen Game-Engines wie Unity3D oder der Unreal-Engine kann man Kräfte, definiert als Vektoren, auf Objekte wirken lassen.

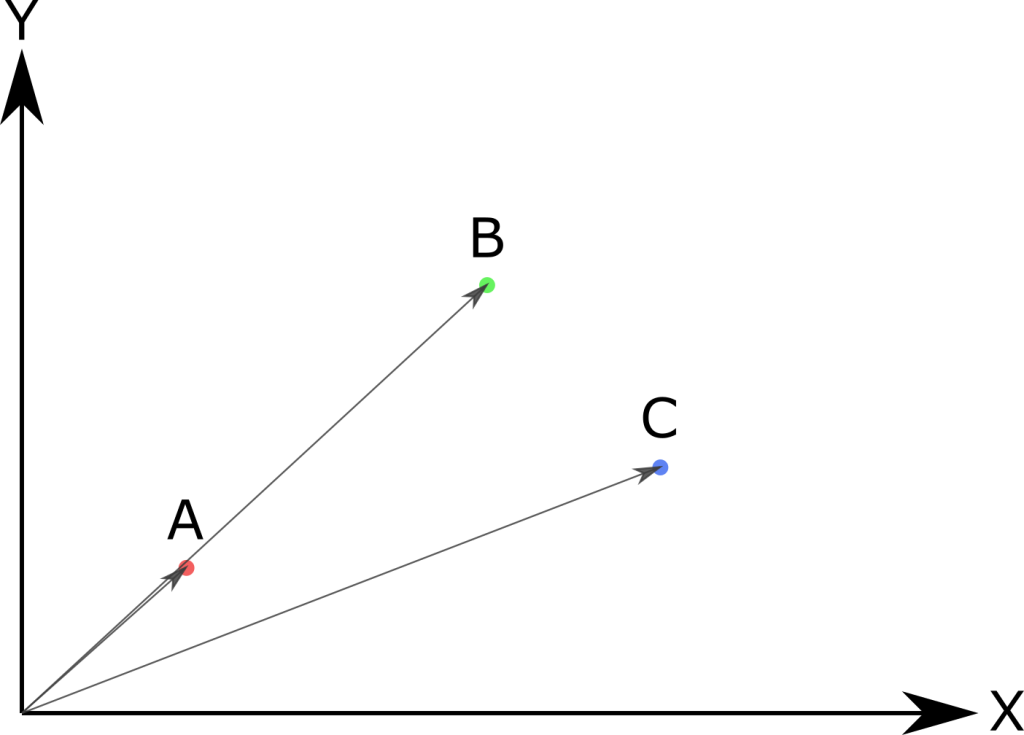
Aber bleiben wir bei dem Punkt im Raum. Wer Spiele entwickelt, muss ziemlich sicher irgendwann den Abstand zwischen zwei Punkten A und B berechnen. Dazu brauchen wir zuerst den Vektor, der von A auf B zeigt, definiert als ab = B – A. Dieser Vektor ab hat im zweidimensionalen Raum zwei Ausrichtungen X, Y im Allgemeinen – bzw. Xab und Yab in unserem Beispiel.

Um die Länge |ab| dieses Vektors zu berechnen verwendet man den Satz des Pythagoras:

|ab| = sqrt(x² + y²)

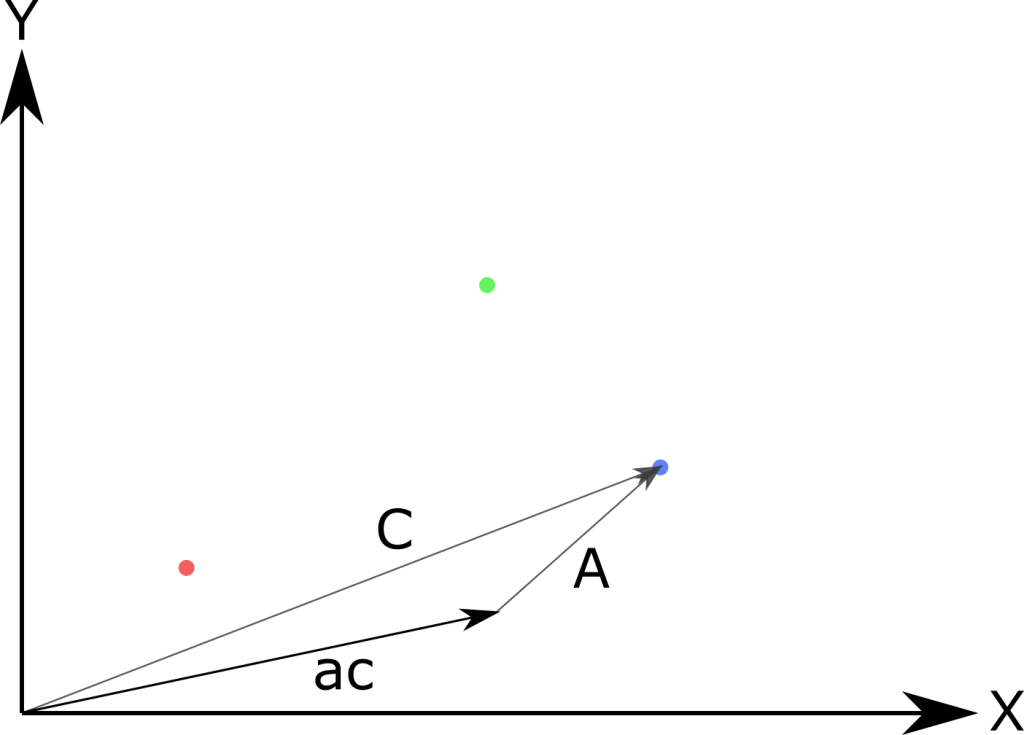
Wenn ab der Vektor ist, der von A auf B zeigt, entspricht seine Länge |ab| dem Abstand zwischen beiden Punkten. Soweit so gut. Aber was ist, wenn ich berechnen möchte, ob ein dritter Punkt C näher an A ist als B?

Jetzt kann ich hergehen und die beiden Längen |ab| und |ac| berechnen. Ist |ab| < |ac| ist B näher an A als C.
Diese Berechnung fordert vier Potenzen, zwei Additionen, zwei Mal muss eine Wurzel gezogen werden und am Ende noch eine Subtraktion. Additionen, Multiplikationen und Subtraktionen sind im Befehlssatz des Rechners vorhanden und in Hardware ausführbar, daher brauchen diese Operationen nicht viel Zeit. Deutlich aufwändiger ist die Berechnung einer Quadratwurzel und es wäre eine große Performancesteigerung, wenn man sich diesen Rechenschritt sparen könnte. Glücklicherweise interessiert uns nicht der absolute Abstand, sondern nur in welcher Relation die beiden Distanzen zueinanderstehen.
Wir können uns folgende Regel zunutze machen: Wenn a > b, dann ist auch a² > b². So können wir unsere Berechnung der Differenz beider Distanzen stark beschleunigen, indem wir beide Seiten der Gleichung quadrieren:

Vektor allgemein: v = (X, Y)

Vektor ab = (Xab, Yab), ac = (Xac, Yac)


Gleichung:
|ab| > |ac|

Entspricht:
sqrt(Xab² + Yab²) > sqrt(Xac² + Yac²)   | ()²

Das wiederum entspricht:
Xab² + Yab² > Xac² + Yac²

Jetzt haben wir eine Formel, die ohne die Wurzelfunktion auskommt und einiges an Rechenzeit gespart.
Moderne Game-Engines liefern bereits die Möglichkeit, einen Abstand zu berechnen, ohne dass die Wurzel gezogen wird: In Unity3D berechnet Mathf.Sqrt(float f) die Wurzel und Vector3.sqrMagnitude() berechnet die Länge eines Vektors bis auf die Wurzelfunktion, was in diesem Fall völlig ausreicht:
B ist genau dann näher an A als, wenn: (B-A).sqrMagnitude() < (C-A).sqrMagnitude().

Ladezeiten von Webseiten optimieren:

Das zweite Beispiel betrifft eine Website. Heute sind die Ladezeiten einer Website ein kritischer Faktor, um das Absprungverhalten der Besucher zu verbessern. Mit einer vernünftigen Internetleitung sollte jede Website im Prinzip sofort geladen werden, allerdings kann es bei unnötig großen Bilddateien und schlechter Internetverbindung gerade auf mobilen Endgeräten in Deutschland zu langen Ladezeiten kommen.
Warum Deutschland beim Internetausbau europaweit auf den letzten Plätzen rangiert, ist für mich nicht nachvollziehbar. Mittlerweile scheint der Glasfaserausbau in Schwung zu kommen, aber auf einer 100-Quadratmeter-Insel in den Schwedischen Schären lädt Netflix bei mir schneller, als hier bei Oma auf dem Sofa und das ist leider kein dummer Spruch …
Aber zurück zum Thema:
Kritischer für die Ladezeiten einer normalen Website sind die Bilddateien und es lohnt sich, diese zu optimieren. Angenommen man möchte ein Bild in Full-HD übertragen, ergeben sich bei einer Auflösung von 1920×1080 2.073.600 einzelne Pixel, die geladen werden müssen. Bei einer PNG-Datei besteht ein Pixel nicht nur aus den drei Grundfarben rot, grün und blau, sondern zusätzlich noch aus einem Alpha-Wert. Der Alpha-Wert definiert die Transparenz des Pixels um den Hintergrund des Bildes auf der Website durchscheinen zu lassen. Die erste Frage bei der Wahl des Bildformats ist somit die, ob man denn wirklich Transparenz benötigt. Wenn nicht kann man einen geringen Qualitätsverlust (keine Transparenz und verlustbehaftete Komprimierung) im Tausch für eine kleinere Datei in Kauf nehmen und auf jpg wechseln. Das spart Ladezeiten und Speicherplatz!

Bei Logos, die im Vergleich zu Fotografien häufig nur aus geometrischen Formen bestehen, kann man noch weiter sparen und statt einer klassischen Bilddatei wie png oder jpg auf die Scalable Vector Grafic SVG zurück greifen. In einer Vektorgrafik sind die geometrischen Strukturen nur mittels Vektoren definiert, was zwei wesentliche Vorteile mit sich bringt: Erstens ist die Datei verhältnismäßig klein, da keine farbigen Pixel gespeichert werden, sondern Vektoren die die Formen definieren. Zweitens kann dank der Vektoren das Logo oder die Grafik verlustfrei skaliert oder mittels JavaScript animiert werden.

Fazit

Wenn von „Grundlagen der Programmierung“ gesprochen wird, denkt man gar nicht unbedingt an Vektoren, sondern eher an kryptische Zeichenfolgen in grüner Schrift auf schwarzem Grund, die von Strebern und Nerds gelesen werden können wie ein normales Buch.
Man sollte sich aber klar machen, dass die Informatik eine Disziplin der Mathematik ist und es letztlich nur darum geht Informationen (Daten) zu interpretieren und zu verknüpfen.
Ich habe mir den Vektor der linearen Algebra als Beispiel ausgesucht, um zu zeigen, wie Grundlagenwissen der Vektorrechnung in den unterschiedlichsten Bereichen der Softwareentwicklung entscheidende Verbesserungen hervorbringen kann.
Neben der Mathematik empfehle ich jedem ambitionierten Softwareentwickler, sich auch mit dem Aufbau eines Prozessors oder Mikrocontrollers zu beschäftigen. Pointer in C/C++ sind ungleich leichter zu verstehen, wenn man weiß, was tatsächlich physikalisch beim Instanziieren eines Datentyps passiert. Dazu wird es mit Sicherheit noch den ein oder anderen Beitrag auf dieser Seite geben -> Newsletter 🙂
Und das ist keineswegs nur trocken Brot. Man stößt dabei auf interessante Technologien, die faszinierende Früchte treiben, was in diesem Beitrag anschaulich erklärt wird! Einfach zu der ersten Antwort mit den zigtausend Votes und dem grünen Haken vorscrollen 😉

PS.: Alle die Informatik studieren wollen und denken, sie würden dann den ganzen Tag programmieren, sind jetzt gewarnt! Es lohnt sich aber, denn zu wissen, was man tut, gibt Sicherheit und Selbstvertrauen. 🙂